Formality of Systems Thinking
Knowledge, unlike "just facts," is something that can be used in different situations, something that can be taken from one project to another. Most often, these are explanatory theories. Facts, on the other hand, can describe specific projects and objects within them. Knowledge about meters as units of measurement is common to all projects. The length of a path in a specific project being 14 meters --- this cannot be applied to other projects, so it is not "knowledge," it is just a "fact."
Logic (rules of reasoning leading to plausible judgments from plausible premises) in science and engineering is not necessarily Boolean/discrete with values of "true" and "false." Modern logic is probabilistic. When using logical inference in rational thinking, the focus was recently on Bayesian probability, not frequency. Now, it turns out that Bayesian probability is not the last word, and it's about "quantum probability" from the mathematics of quantum physics, although this probability has no relation to particle behavior in the micro world but characterizes different scales in thinking (sometimes referred to as quantum-like thinking).
Modern logic uses probabilistic (Bayesian and quantum-like) reasoning, and experiments ultimately do not prove or refute something but shift the likelihood of plausibility. Life is not made up of "truths" and "lies," it is assessed by statements about probabilities, and even more so: life consists not so much of statements but of actions chosen in a rational way - statements here play an auxiliary role! We have already discussed that "a building consists of bricks" - this is a completely true logical statement, but in real life, it can lead to having to discuss the construction of the building by pointing out the position of each brick. It would be much simpler to unite the bricks into walls and then discuss the position of the walls in the building - and systems thinking works with this "convenient grouping." Not everything that is logically correct will be appropriate in systems thinking; a connection with life is required - with some methods/practices/cultures/styles of work for which discussions are conducted.
But now we will consider another branch of the discussion of the relationship between systems thinking and logic. Is systems thinking formal/strict (expressed in symbolic form, available for rigorous logical inference through values of "true" and "false")? Or is it informal, i.e., intuitive and thereby more prone to error? Another formulation of the same question: can it be considered that systems thinking requires strict/formal typification of its objects, as in mathematical logic?
The main thing that needs to be discussed here is the presence and importance for transdisciplinary thinking (and systems thinking is transdisciplinary) of informal, intuitive, and inexpressible in words and other signs knowledge in distributed (for example, neural network-based - in a living brain or in AI computer systems) representations, including distributed knowledge about systems. This is the quick thinking knowledge S1 by Kahneman. Today, such knowledge can be possessed not only by people with a "wet neural network" (studied by Kahneman), but also by computers programmed to work within the connectionist/neural network paradigm. Modern advances in artificial intelligence are associated precisely with the development of this "computer intuition" (rather than the development of logical programming languages) within machine learning in general and deep learning in particular.
In the connectionist paradigm, knowledge is represented as existing not as a set of related relationships between discrete concepts from formal logic but as distributed among a multitude of specific simple homogeneous elements (today usually neurons in neural networks, both artificial and natural). This is the rather powerful concept of distributed representations in contrast to local/symbolic representations. Semiotics as part of semantics deals with symbolic representations, while distributed representations are currently being studied in AI projects, with a particular focus in the field of deep learning, dealing with hierarchical distributed representations (for example, in the form of a multi-layer/deep neural network).
The idea that knowledge/information can be represented in terms of distributed representations through information physics theories can easily be generalized to the recognition of scale-free knowledge spread throughout the entire universe (including human knowledge). Human thinking uses a neural network for thinking, and therefore largely works with distributed rather than local representations, although it can organize a "virtual logical machine operating with types and relationships between them" on a neural network, i.e., the brain can slowly and with errors function as a classical logical computer.
The human brain poorly functions with formal/mathematical/strict/symbolic representations of knowledge and facts; its computations are probabilistic and require verification. Animal brains can hardly work with symbolic/sign-based/local representations; skill in working with signs is precisely what sets humans and animals apart.
Modern machine learning and artificial intelligence systems use principles similar to the functioning of the human brain. Today, knowledge is understood not only as formal/strict mathematical models. Combining formal, "scientific" knowledge work methods with "informal" intuitive methods in neural networks (artificial or natural - it doesn't matter for the human brain) represents a scientific and technical frontier, which we will not touch upon in our course. In any case, we can greatly reduce errors in informal probabilistic reasoning by simply giving more time for calculations. This is currently a hot topic in research on large language models - can we seek an answer to a slightly modified question several times to get a more reliable and error-free answer? Yes, we can![1].
Daniel Kahneman claims[2] that humans have two modes of thinking: fast, low-cost intuitive S1, and slow, high-cost conscious S2, which comes into play when problems arise using "fast" intuitive thinking. S2 represents the ability to engage in sequential acts of S1 thinking and thus the possibility of logical sequential step-by-step thinking.
In fact, there is a whole spectrum of thinking from intuitive informal through probabilistic (with some estimates of these Bayesian or quantum-like probabilities from various sources of a priori evidence and experimental data) to classic formal based on mathematical logic. Here the scheme by Prapion Medvedeva is illustrated, illustrating this full spectrum (all this was explained in the "Modeling and coherence" course):
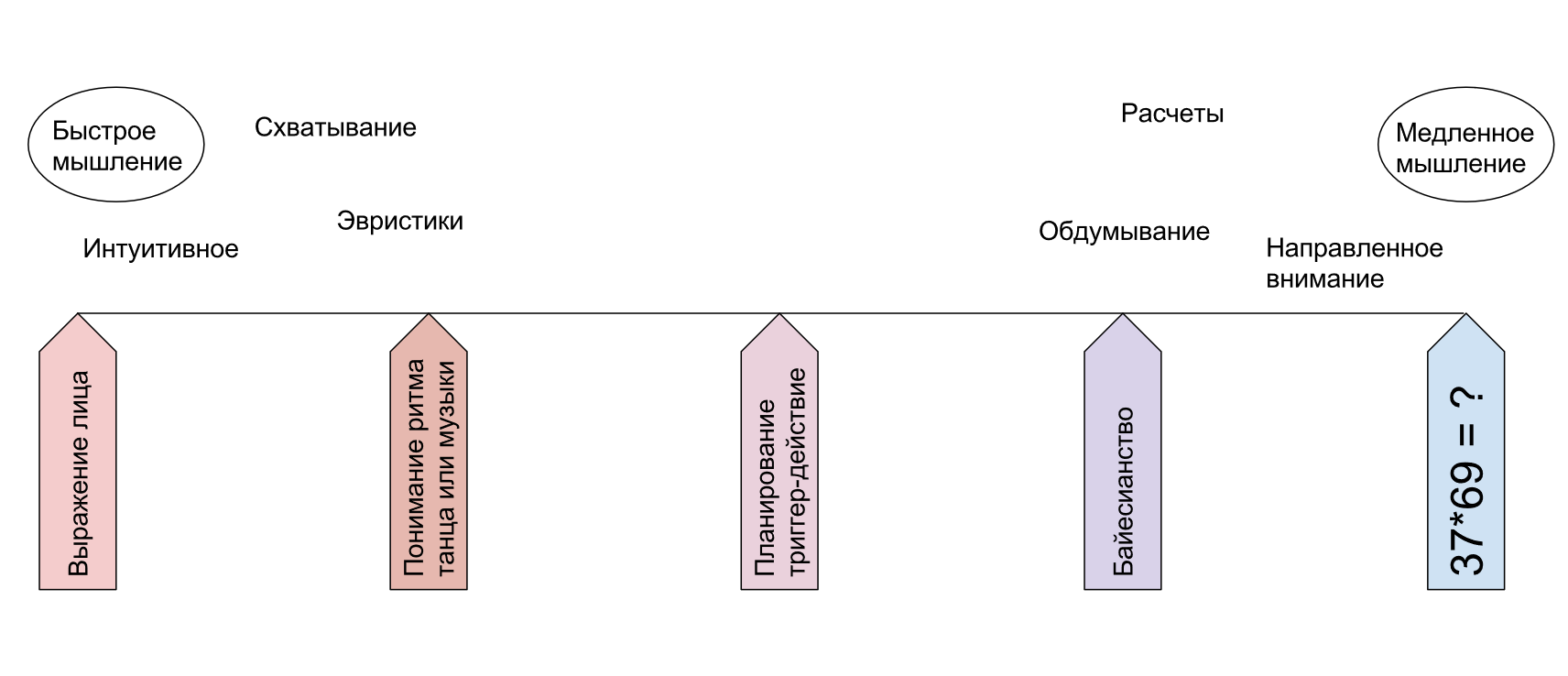
Usually, intuitive hunches at the "sensory" level are pulled out as explicitly formulated heuristics, and heuristics are tested by criticism: by logic (including Bayesian probability logic or quantum-like logic). If the hunches are confirmed, formal slow thinking S2 about a certain type of problems can then be trained (in the process of solving a multitude of tasks) so that it becomes automatic and "intuitive" S1, requiring no special mental effort, and the solution to this class of problems moves from the part of the spectrum with "deliberation" and "directed attention" to the area of fast intuitive without particular involvement of the expensive resource of concentration. Physicists develop "physical intuition", mathematicians develop "mathematical intuition", systems thinkers develop "system intuition". The brain is plastic, the neural network of the brain is well trained (and recently these "intuitive" reasonings began to be gradually transmitted to neural networks in computers).
With a description of options for automatic query selection, Jason Wei intuition https://arxiv.org/abs/2311.16452 Jason Wei https://twitter.com/_jasonwei/status/1729585618311950445 ↩︎
Daniel Kahneman, "Thinking, Fast and Slow", https://en.wikipedia.org/wiki/Thinking, Fast and Slow ↩︎