Concept
Let's call this property of passing a certain threshold of understanding, after which it's hard to remember the difficulties, metanoia. It's an amazing word, try to write it in different cases, and even in plural, you'll get very interesting effects. This term comes from religious practices and means "a change of mind," a complete break from past and current thinking. You're working, attending some seminar, and it seems like your thinking is not quite what priests expect from you. Then suddenly at some point, a switch clicks - and you demonstrate to everyone that your thinking is the same as that of a clergyman, from this moment you are "real," not pretending. This is what was called "metanoia," a Western term for enlightenment. The word "metanoia" was recommended to be used instead of the word "education" by the system management guru Peter Senge[1], because the word "education" from his point of view is already worn out and does not signify a fundamental change in thinking as a result of education. He borrowed it from psychologists who used it to denote radical positive changes in personality[2]. We don't like the religious connotations of metanoia, but the phenomenon denoted by this word, "forgetting the difficulties of learning," is quite secular.
When metanoia happens, in a new state of his thinking, with "new tracks in the brain," a person (or in a more general case - an agent of various natures) completely doesn't understand what the problem was before with the "old tracks of thinking." Let's imagine: I know the Earth is flat, I argue for a long time that the Earth can't possibly be round, but at some point I am convinced. And in each of my projects, I initially act automatically as if the Earth is flat, then by willpower I remember that rationally it should be round, then I do this automatically, and at the same time, I see a thousand proofs of this roundness of the Earth. And at that moment, I can't understand why I believed the Earth was flat. Rationally, I can remember that I once thought the Earth was flat. But I can't understand how I transitioned from the state of knowing the "intuitive theory" to possessing the "counterintuitive theory." And that's why I can't realize the learning actions needed to achieve this metanoia of the roundness of the Earth in my students. But the fact of paying attention to this past metanoia (bringing it to consciousness) gives a chance to understand. Creating the right exercises for students to achieve this metanoia is a difficult but possible task. Developing an adequate course based on an existing theory can take a couple of decades, and if besides the exercises, a new theory needs to be created, then it can take hundreds of years like in the transition from the Ptolemaic to Copernican understanding of planetary motion. All these considerations about the difficulty of creating theory/explanations/knowledge and a training course to achieve fluency/metanoia in students' thinking fully apply to systems thinking, all methods of the intel-stack, and applied engineering methods.
Special attention should be paid to the fact that in the case of metanoia, it usually refers not to teaching any thinking and action methods, but to "counterintuitive" ones, to which the brain particularly resists because in this case it "intuitively knows" how things should be, and actively resists new knowledge! It's much easier to teach something anew, but if you've already picked up some "folk intuition" somewhere, then teaching you something more effective will be very problematic: you'll have to go through metanoia, which requires having a documented model of the goal thinking, organized into a training course sequence of exercises, time to complete these exercises, as well as a considerable collectedness - because all the intuition of the students will show that they are being taught some nonsense! There is almost no chance to go through this metanoia "on your own" unless you are a genius. So, you'll never teach yourself explanations about the Earth's roundness if you adhere to the theory of a flat Earth. In this case, your chance is only to attend courses where you will literally be forced to familiarize yourself with the arguments about the roundness of the Earth, and then be trained (against your will! Just forced!) to fluently use this knowledge.
Counterintuitiveness can be found in the simplest actions. At school, you were taught to jump over a bar using "scissors" - you run up and jump. But if you need to jump very high, then after running up to the bar, you need to turn your back to it and jump back-upward (Fosbury Flop, invented in 1968[3]).
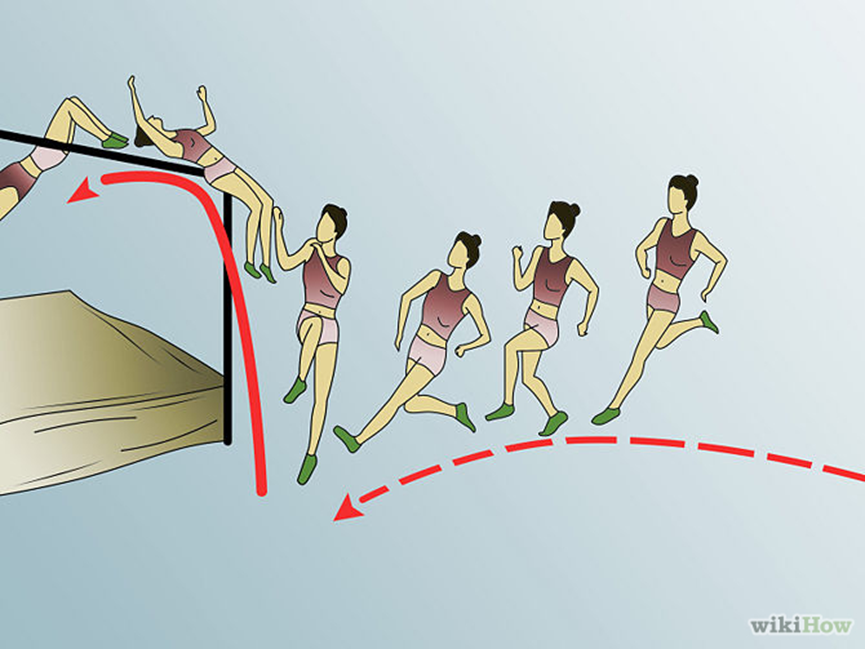
This is absolutely counterintuitive but allows you to jump over a two-meter bar. You need immense trust in your coach to start training this jump - because at that moment it seems that many, many workouts will allow you to overcome additional tens of centimeters with "scissors" or a "roll," which is not the case. And then there will be metanoia: you won't understand why people even jump over bars using other techniques - even if you don't remember that Dick Fosbury started such jumps and people only began doing it just a year before landing on the Moon in 1969. And we're talking about what people have been doing for millennia: high jumping!
In thinking, there are similarly counterintuitive methods that allow thinking to follow the sports motto: "faster, higher, stronger," leading to "high-performance sports." Systems thinking - is a set of specific, invented by different people, specific counterintuitive thinking techniques that allow thinking to be stronger (more universal and efficient) than its previous, "folk" variants. In particular, systems thinking - is primarily an effective way to manage attention in a project, it allows you to standardly identify in the project objects worthy of primary attention. You will know what is important in the project before even starting on it! The concepts of systems thinking set the types of important objects that you will have to find in the project, it allows you not to wander with the hope that you will sooner or later encounter something important, but to actively search for and find this important thing.
The main substantive metanoia of systems thinking is that you start thinking about the world as consisting of nested part-whole systems that interact with each other, and some systems are created and developed by other systems, establishing a relation of creation. In the third generation, this is further supplemented with an understanding of the evolutionary timescale and the inevitability of conflicts between systems of different levels.
Understanding a system not as "any object we consider" but as a "system from a systems approach" turns out to be extremely counterintuitive, thus requiring special training and subsequent long practice of such systems thinking.
So, "intuitively," when trying to talk about something (for example, about borscht, the Ministry of Attack, a quantum computer), people talk primarily about the parts of the discussed object (borscht composition, organization of the Ministry of Attack, computer components). In systems thinking, it's the exact opposite: the discussed system-object is immediately declared a part, and the story is primarily about the environment at the moment of the functioning/operation of the target system. This is the situation of lunch and digestion when it comes to borscht, the attack situation in the Ministry of Attack, the use situation of a quantum computer: borscht, the Ministry of Attack, and the quantum computer will only be parts of their usage situations. It's only after understanding the systemic environment (what surrounds the borscht during lunch and then during digestion, what surrounds the Ministry of Attack during the attack, what surrounds the quantum computer during its use) that the object of interest for the systems thinker will be from the inside, the parts of the system. First - what happens outside the system boundary, and only then - what happens inside! This is very, very counterintuitive!
In mathematics, the term "intuitive" is often replaced by the term "trivial" - the ability to be repeated by "any" person in this community (since AI mathematicians have not worked seriously yet), and non-triviality - the impossibility of repetition (thanks to mathematician Roman Mikhailov for discussing this issue). Demonstrating something interesting due to non-triviality makes this "something" trivial through a couple of cycles of training interested parties because the definition of "intuitiveness/triviality" and "counterintuitiveness/non-triviality" implicitly includes the moment "right now." Any "counterintuitive/non-trivial" of one generation becomes "intuitive/trivial" for another generation of thinkers. This "triviality" can easily be added to the list of synonyms for "intuitiveness." Intuitiveness/triviality and counterintuitiveness/non-trivial are "moving targets," assigning these types to some objects is quite dynamic, the result significantly depends on time.
Who knows, maybe today's systems thinking for future generations of people and thinking machines will be "folk," "intuitive," "trivial," and it will need to be overcome, to achieve metanoia in a completely differently structured thinking. But for now, systems thinking is deeply counterintuitive in its current form, mastering it is difficult, and metanoia is inevitable.
In our discussions, we use both the everyday and non-everyday meanings of the word-term "intuitiveness." In everyday sense, "intuitiveness" often implies not the result of rational logical reasoning, but the use of "hunch" - getting the result of reasoning with insight, inspiration, illumination, and this result can be quite non-trivial. We call such results of thinking "counterintuitive," meaning they are non-trivial, not easily reproducible by various people, these results do not belong to "common knowledge," popular thinking automatisms, typical intuition of the surrounding people, as well as one's own intuition. But in our course, we often refer to the second "folk" dictionary meaning of "intuitiveness" when we talk about quick "intuitive" thinking S1. We hope that from the context, students will understand which meaning the authors of the course had in mind in each case of using the term "intuitive."